14-Sept-2016: Trajectories

PURPOSE:

We must use our knowledge of projectile motion in order to predict the landing point of a ball upon an incline.

INTRODUCTION:

Picture a ball rolling along a table and falling off an edge onto the floor. This is essentially the situation that our group was presented with. With this in mind, we are trying to measure the horizontal and vertical distance traveled by a ball in projectile motion. Given these measurements, we shall use kinematics equations to calculate the initial horizontal velocity of the ball. The initial velocity will give us insight into the ball's trajectory. The question now becomes:

If we were to place an incline of angle theta in the trajectory of the ball, where would the ball land along the incline? 

In other words, picture the same ball rolling along a table and falling off the edge onto a ramp. We must predict the ball's point of impact along this ramp. To do this, we must derive an equation that illustrates a relationship between the initial horizontal velocity of the ball and the distance, d traveled along the incline.

APPARATUS: PART 1:

1) We set up the apparatus as shown:

Diagram of apparatus

1) Secure Aluminum "v-channel" #1 to the table. We kept ours in place with lumber, metal weights, rails, and some tape.

2) Line up Aluminum "v-channel" #2 such that it flows into the the first "v-channel" at an angle. Make sure that the angle of incline for the second "v-channel" is not too steep to ensure the steel ball does not bounce when it hits the transition between the two channels.

3) Line up the ring stand with Aluminum "v-channel" #2 and use the clamp to secure them together. In reality, we just secured the clamp to the ring stand and allowed the "v-channel" to rest on top of the clamp. Adjust the angle of incline as needed.

4) When you are done, the apparatus should look something like this:

Fully assembled apparatus

PROCEDURE: PART 1:

1) Launch the ball from a point near the top of the inclined ramp. We marked our starting point with tape to keep it consistent. Notice where it hits the floor.

2) Tape a piece of carbon paper to the floor where the ball landed. We placed a blank piece of paper underneath the carbon paper so it would have a surface to mark on afterward. 

Carbon paper secured to floor

3) Launch the ball five times from the same place you launched it initially. Ensure that the ball lands in virtually the same place every time. 

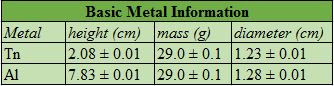
4) Determine the horizontal and vertical distance the ball traveled during its launch. We measured these distances with a meterstick. We also included our uncertainty in each value:

5) Determine the launch speed of the ball using the measurements you obtained. In this case, we utilized the average delta x value for our calculations. Note: Don't forget to convert from centimeters to meters first. Here are our calculations: 

Launch speed calculations

APPARATUS & PROCEDURE: PART 2:

6) Imagine attaching an inclined wooden board to the edge of the table such that now the ball, launched from the same place as before, will strike a distance d along the board, like so:

7) Derive an expression that would allow you to solve for d given that you know Vo and alpha. Note: I used theta instead of alpha to signify the angle measure. Additionally, don't round any of your intermediate values--e.g. Vo and theta. Here is our derivation of this expression with its corresponding calculation of d:

Note to self: Use pen next time! Too light!

7) Now it is time to test our predictions. Place a wooden board such that it touches both the edge of the table and the floor. This will act as a ramp for the ball as depicted in the previous diagram. Once you have reasonably adjusted the slope of your ramp, secure it to the floor by pushing some weights up  against it and taping them to them ground. Finally, measure the angle of the board. We used an iPhone app to make this measurement. This is how ours looked:

8) Attach a piece of carbon paper to the board such that it is within the vicinity of where you predicted the ball would land. Now run the experiment, launching the ball five times from the same spot. In our case, we only had enough time to run it once.

9) Determine the experimental value of your landing distance d with its corresponding uncertainty. For example, according to my group-mate, our experimental landing distance d was 75.0 ± 0.1 cm. Here are our final findings:

CONCLUSION:

It appears that our theoretical calculations were fairly close to our experimental values. In fact, our predicted value for the landing distance d was less than 4 centimeters away from the one we measured experimentally. However, this does not hide the fact that there are a number of factors that have contributed to the inaccuracy of our measurement of d. One of the most prominent causes that come to mind is human error. This is because there will often times be a misreading of measurements from tools such as rulers and calipers. The marking are small, and minute changes in perspective can cause some group members to see one measurement and others group members to see another; such was the case with our group from time to time. Additionally, there were certain assumptions we had to make about the world that could have affected the accuracy of our calculations. For example, when carrying out our calculations for d and Vo, we assumed that acceleration due to gravity equals -9.8 m/s². In order to be more precise, we could have utilized the value -9.81 m/s² instead and perhaps increased the accuracy of our calculations. Lastly, if our group had run more trials at the end of the experiments, we could have gotten a more accurate understanding of the experimental value of the landing distance d. With an average of these trials, we also could have a better grasp on how accurate our theoretical values were in comparison to the values we measured.

GROUP MEMBERS: Matthew I., Xavier L., Billy J.

7-Sep-2016: Propagated Uncertainty

PURPOSE:

To calculate the propagated error in measuring the density of metal cylinders.

INTRODUCTION:

We are simply measuring the mass, height, and diameter of two metal cylinders in order to determine the propagated uncertainty inherent to their measurements. To do this, we will utilize the sum-of-squares method for the total differential of the density function: mass/volume. Where volume = ∏r²h. This method will allow us to see how much uncertainty there is in our calculation of the density of a given metal cylinder.

PROCEDURE:

To do this lab, you will need the following materials: calipers, scale, and two metal cylinders.

1) Record the B.M.I. (Basic Metal Information) of your two metal cylinders using the calipers and the scale. These measurements include height, mass, and diameter. Make sure to include the uncertainty in each measurement as well. It will come in handy for our final calculations. These are the measurements we recorded:

2) Derive an expression for the density of a cylinder in terms of the three variables we measured. This will allow us to find the total differential in terms of h, m, and D. Note: the terms dm, dh, and dD represent the uncertainty in mass, height, and diameter, respectively. Finally, use the sum-of-squares method to derive an equation for the propagated uncertainty in the density of a given metal cylinder. Below is the derivation of our equation:

3) Calculate the propagated error for each of your density measurements. It is simply plug-and-chug from here on out. Here are our propagated error calculations for the tin and aluminum cylinders:

CONCLUSION:

According to our calculations, it appears that our measurements for the density of the aluminum cylinder were much more accurate than that of the tin cylinder.This difference in uncertainty was most likely the result of human error. For example, an inaccurate reading of the calipers could have resulted in a higher uncertainty in our calculations. Another possible source of error is faulty equipment. For instance, the scale we used would often oscillate between 29.0 and 29.1 g whenever we measured the mass of our cylinders. This could be an indication that our equipment was not as precise as we needed it to be. 

GROUP MEMBERS: Matthew I., Xavier L., Billy J.

29-Aug-2016: Find Nemo

Deriving a power law for an inertial pendulum

PURPOSE:

We are trying to find a relationship between mass and period for an inertial pendulum. Furthermore, we want to use this information to create an equation that will accurately predict the mass of any object we place on top of this pendulum.

INTRODUCTION:

Our task is to accurately measure the mass of a given object. The only caveat is that we are not allowed to use a spring scale, balance, or any other measuring device that utilizes the Earth's gravitational pull in order to determine mass, Therefore, we must make use of indirect methods to acquire this measurement. More specifically, we must make use of an inertial balance to measure inertial mass by comparing an object's resistances to changes in motion. Firstly, we will use the inertial pendulum to directly measure the periods of a set of pre-determined masses. Secondly, we will relate these quantities using a power-type equation. Thirdly, we will utilize Logger Pro to help us determine any unknown variables in our equation. Lastly, we will use this mathematical model to calculate the mass of an unknown object.

APPARATUS:

1) We used a C-clamp to secure the inertial pendulum (tray) to our table. Then, we put a thin piece of tape on the end of the tray.
2) We set up a photogate so that the thin piece of tape would pass completely through the beam of the photogate whenever the tray oscillates. The photogate is what allows us to measure the period of the oscillating pendulum.
3) We set up LabPro on our computer so we could record the period in real-time.

the fully assembly apparatus

PROCEDURE:

1) We recorded the period with no mass on the tray.
2) We recorded the period with 100 g on the tray. We went all the way to 800 g, in 100 g increments. Here is a picture of one of our measurements:

Graph of period measurements with respect to time

3) After each measurement, we recorded our data in a table:

4) Next, we related mass and period using the power-type equation:

T = A(m+Mtray)^n      (We used m+Mtray because the mass of the tray is always present.)

This gives us three unknowns we need to solve for: A, Mtray, and n.

5) We took the natural log of both sides of the aforementioned equation to obtain:

ln T = n ln(m +Mtray) + ln A

Since it looks very similar to  the linear form y = mx +b, we can plot it in LabPro as such. 

6) We made a plot of ln T vs. ln(m +Mtray). This gave us a line of slope n and a y-intercept equal to log A (assuming our value of Mtray is correct).

Unfortunately, our group's initial value for Mtray was not so exact. In order to determine the correct Mtray, we needed to do a linear fit of our data and try different values for Mtray until we achieved a perfectly straight line plot. To get a straight line, we needed to make sure that the correlation coefficient was as close to 1.000 as possible. The following two graphs display linear fits of the aforementioned equation whose values of Mtray are consistent with a correlation value ~1.000.

Graph of ln T vs. lm (m +Mtray) -- Lower Bound

Graph of ln T vs. lm (m +Mtray) -- Upper Bound

Based on these graphs, our group was able to discern that there was actually a range of values for which the correlation coefficient would be very close to 1. This would seem to suggest that there are a number of plausible values for Mtray--when in reality, the mass of the tray is constant. This indicates that our mathematical model has some inherent uncertainty that could affect the accuracy of our calculations when we attempt to determine the masses of our unknown objects.

EXTENSION:

Using the values of A and n that correspond to our upper and lower bounds of Mtray, we finished constructing our mathematical model and used the resulting equation:

e^[(ln T - ln A)/n] - Mtray(1,2)

to determine the mass of two objects: a smartphone and a stapler. Below is a table of the information we collected from the graphs. Mtray1 represents the lower bound while Mtray2 represents the upper bound. The measured mass is the mass of the objects recorded from a scale. We used these values as a point of reference for the accuracy of our calculated mass.

ln A and n values collected from linear fit graphs (top).
Period (T) and mass (g) collected for each object (bottom).

Here are our calculations for the masses of the two objects using the upper and lower bounds--with their corresponding ln A and n values:

CONCLUSIONS:

Overall, it appears that our calculations for the mass of the two objects were not as accurate as we were hoping for. For example. the lower bound values yielded a calculated mass for our first object (smartphone) that was about 6 grams higher than the gravitational mass we measured on the scale. In other words, the actual mass of the phone would not even be within the range of values we calculated. Moreover, a similar trend emerged when we calculated a range of values for the mass of the second object--a stapler. In fact, according to our calculations, the mass of the stapler ranged anywhere from 374.0 g to 375.8 g. However, when we went to determine the mass on the scale, it read 369.0 g.This uncertainty could be the result of several factors. For instance, we could have recorded a more accurate measurement for the period of the object instead of leaving it at one significant figure. Moreover, this error could have also resulted from the inconsistent placement of objects on the tray. Not every object is built the same way, thus, the weight of said object may not always sit evenly distributed on the tray. For instance, a majority of the stapler hung off the sides of the inertial pendulum because it was far too large to fit inside the tray itself. This could lead to inaccurate measurements for the period of the object, and--by extension--the mass of the object as well. Furthermore, as was previously stated, we utilized a range of values for Mtray, which had some inherent uncertainty in our calculations for the masses of the objects we chose,